Berechnungen mit dreidimensionalen Koordinaten (x/y/z)

Hinweis 1

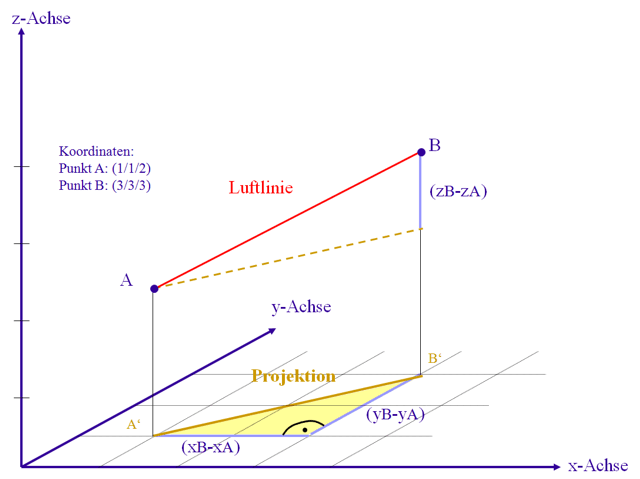
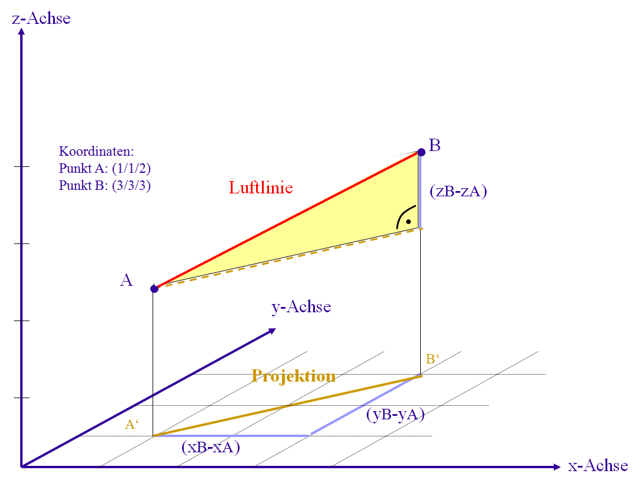
Die direkte Verbindungsstrecke zwischen zwei geografischen Punkten A und B nennt man Luftlinie. Würden Lichtstrahlen senkrecht auf die xy-Ebene einfallen, so wären die Punkte A′ und B′ die Schattenpunkte von A und B und die Projektion wäre der Schatten der Luftlinie

Hinweis 2

Die Projektion liegt in der xy-Ebene und du benötigst für die Berechnung ihrer Länge deshalb nur die x- und y-Koordinaten der Punkte A und B. Betrachte das gelbe Dreieck in der xy-Ebene. Es handelt sich um ein rechtwinkliges Dreieck. Die Projektion ist die Hypotenuse. Die beiden Katheten sind die Unterschiede der x- und y-Koordinaten der Punkte A und B. Mit dem Satz des Pythagoras rechnest du die Projektion aus. Für unser Beispiel gilt:

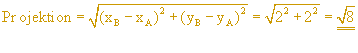
Hinweis 3

Die Projektion ist die Horizontaldistanz der Luftlinie. Wenn du die Länge der Projektion kennst, dann benötigst du nur noch den Unterschied der z-Koordinaten der Punkte A und B um die Luftlinie zu berechnen. Schau dir nun das gelbe Dreieck in der Grafik unten an. Es ist wiederum ein rechtwinkliges Dreieck. Die eine Kathete ist gleich lang wie die Projektion, die andere Kathete ist der Unterschied der z-Koordinaten. In der Grafik ist ersichtlich (zB-zA)=1.

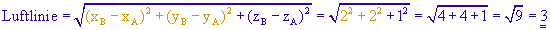
Hinweis 4

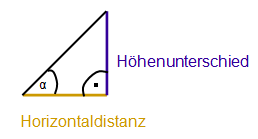
Und was versteht man unter "Steigung"? Schau dir nochmals die Grafik und das gelbe rechtwinklige Dreieck an. Die Steigung ist nichts anderes als das Verhältnis von Höhenunterschied und Horizontaldistanz.

Wann ist eigentlich eine Steigung 100% und wie gross ist dann der Steigungswinkel α? Genau dann, wenn die Horizontaldistanz und der Höhenunterschied gleich gross sind. Du erkennst unten, es handelt sich um ein gleichschenkliges Dreieck mit α=45°.